Why low interest ≠ low cost?
When 0% interest isn’t.
· 18 min read
Take a look at these loan offerings from banks operating in Singapore. Notice something?




All of them scream a low, shiny interest rate in giant fonts, but the real cost of borrowing is either buried in tiny typefaces or hidden in the fine print altogether.
Banks love to shout about the “teaser” rate because it looks cheap. What they don’t want you to notice is the effective interest rate (EIR), which is the actual rate you’ll pay once fees, compounding, and payment structure are factored in.
So what’s the deal here? And why is the “0%” or “low interest” rate you see in an ad almost never the rate you actually end up paying?
One dollar today > one dollar tomorrow #
A one dollar bill you receive today is, at present, worth more than the same one dollar bill you will receive tomorrow. On face value, this is crazy talk. After all, the value written on the two bills, i.e. the face value, is exactly the same. This concept is crucial when we think about loans later. But first off…
You’re selling an apple for one dollar. To avoid muddying the waters, let’s say there’s no inflation, so the same apple would be worth one dollar even 10 years from now.
- A customer buys an apple on Day 1 doesn’t have cash, so he hands you a legally binding signed note stating “the bearer shall receive one dollar on Day 2”.1 Let’s assume the customer is an upstanding guy who always pays his dues on time.2 Fair enough, you’ll accept it.
- Now imagine the next customer hands you a note promising one dollar on Day 30. Less appealing, but you begrudgingly accept it.
- Another equally upstanding customer does the same, but promises payment on Day 3000"? Forget it.
Intuitively, the note promising to pay you on Day 3000 might as well be toilet paper. It’s too far in the future. You might even refuse to sell the apple in exchange for this. Meanwhile, the note promising to pay you on Day 2 feels basically equivalent to receiving an actual one dollar bill on Day 1, though you likely still prefer the latter. It feels as if the further the payment date is from Day 1, the less you prefer and value that note!
But on face value, all the notes given by all customers promise to pay exactly one dollar. Why do you express any preference for one note over the other at all?
The instinct to prefer a dollar now over the same dollar later is called time preference. It almost sounds trivial, but this is a psychological and philosophical concept at the core of all of finance, from loans to investments to retirement planning. All the supposedly rational, coldly-calculating, and self-interested machinery of finance is built on this very human instinct: I’d rather have my damn money now than later.
Calculating time preference #
If we stop here, it’s psychology or philosophy. To become finance, we need to quantify stuff.
Looking back at the apple example. Deep down, we can intuit that a note promising a dollar at a later date is worth less. How much less? To frame it differently, how much more would you charge for the apple before you accept it as fair?
A promise for one dollar on Day 2 has to be worth less than one dollar, so you would naturally charge a factor of \(1 + r/365\) more for the same apple,3 for some small \(r > 0\). This means the buyer has to hand you a note promising to pay \((1 + r/365)\) dollar on Day 2.
Day 5? A factor of \((1 + r/365)^5\) more. Day 3000? That is \((1 + r/365)^{3000}\) more.
The \(r\) here is called the discount rate or sometimes just the interest rate, typically expressed as an annual rate. It’s the same idea, just framed differently. This represents how much you discount a future payment or cash flow relative to its nominal or face value.
The rate used depends on the context. As a fruit seller, you might not have much patience for future dollars, so you might personally demand4 a discount rate of, say, 20% per annum. By Day 3000 the buyer would have to cough up \(\left(1 + 20\%/365\right)^{3000} \approx 5.17\) dollars. The 517% markup reflects the price of your impatience, and it has nothing to do with inflation.
We call the increased face value of 5.17 dollars the future value, while the one dollar sale price today is the present value. This gives rise to the following relationship between the future value, the present value, the interest or discount rate, and time \(t\): \[ \mathit{FV} = (1 + r)^t \mathit{PV}. \]
Loan as a promise of future cash flows #
Similar to selling an apple in exchange for a note promising future dollars, a loan is really just a product sold by the creditor in exchange for a promise of future cash flows by the debtor. The only mildly noteworthy part is this product happens to be a pile of cash handed in lump sum instead of an apple.
Think of \(L\) as the apple’s price in the previous example. Now instead of a one-time future payment, the buyer promises you a series of future payments in exchange for the apple. Suppose the buyer intends to pay back the loan in \(N\) fixed instalments with amount \(c\). How much more do you charge this “apple” before you accept it as fair? If \(r\) is the interest per period (not necessarily annual), then we have to
- discount each cash flow according to \(r\) and the time it occurs, and
- sum up the discounted cash flows.
The sum must equal to the price of the “apple” \(L\), so that you feel indifferent to receiving the series of future cash flows versus just receiving a lump sum of \(L\) today. So the logic is simple: discount everything, add it up, and if it equals the loan amount, you’ve priced it fairly. Formally: \[ L = \sum_{k=1}^N \frac{c}{(1 + r)^k} = \frac{1 - (1 + r)^{-N}}{r} c. \] Solving for \(c\), we obtain \[ c = \frac{r}{1 - (1 + r)^{-n}} L. \] This is exactly the mortgage formula previously described here!
In general, the future cash flows don’t have to be fixed, and they don’t have to occur at regular intervals. Some loans have variable instalments, balloon payments, or fees and cashbacks sprinkled in. To handle all that chaos in one neat equation, we assign a single “all-encompassing” interest rate \(r\) to make the present value of all promised payments exactly equal to the loan you got upfront: \[ \boxed{L - \sum_{k=1}^\infty \frac{c_k}{(1 + r)^{t_k}} = 0} \] where \(c_k \in \mathbf{R}\) are the cash flows occurring at times \(t_k \ge 0\) for all \(k \in {1,2,\ldots}\).5
Call this the master equation of lending if you like. Solve it for \(r\), and you’ve found the internal rate of return (IRR). For consumer loans, the Monetary Authority of Singapore (MAS) requires banks to disclose the effective interest rate (EIR), which is essentially this same number expressed on an annual basis. In any case, this is the number that really tells you how much your loan costs, regardless of what the advertisement shouts in bold type.
This equation looks abstract, but in a moment we’ll use it to tear apart some of those glossy ads and see what the loans really cost.
IRL loans dissected #
Trust Bank’s personal loan #
Let’s bore into Trust Bank’s personal loan offering as of Aug 2025, consisting of an advertised rate of 1.99% and a disclosed EIR of 3.80% (annualised):

Like most personal loans sold in Singapore, the “teaser rate” of 1.99% is misleadingly advertised as an “interest rate” when it really isn’t. Trust Bank otherwise doesn’t charge extra fees or give cashbacks. Here’s what the teaser rate really is about.
Let \(L\) be the loan balance, \(\rho\) be the per-period “teaser rate”, and \(N\) be the loan tenure expressed in number of periods. Lenders tend to quote the “teaser rate” per annum, so to find \(\rho\) we must divide the teaser rate by 12. The lenders then take the loan amount, slap on \(\rho L\) as the interest cost per month, and then spread that cost evenly across the instalments. Formally, the per-period payment is \[ p = \left( \rho + \frac{1}{N} \right) L. \] See how this is different from how mortgage payment is calculated? Set \(L = 100000\), \(\rho = 1.99\% / 12\) as a monthly rate, and \(N = 40\) in number of months, then \(p \approx 2665.83\), which matches what Trust Bank’s online calculator spits out.
What’s the real cost or interest rate (i.e. EIR) of this loan? Using the master equation of lending presented earlier, we find \[ L - \sum_{k=1}^N \frac{p}{(1 + r)^k} = 1 - \left( \rho + \frac{1}{N} \right) \sum_{k=1}^N \frac{1}{(1 + r)^k} = 0. \] Simplifying further, \[ \rho + \frac{1}{N} = \frac{r}{1 - (1 + r)^{-N}}. \] We can proceed to solve for \(r\) numerically as there’s no nice closed form solution for this. We’ll describe how this can be done later. For now, take it as verified that the EIR is indeed \(r \approx 3.80\%\) annualised.6 This is what you’re really paying if you take on this loan. Notice that the EIR isn’t affected by \(L\).
DBS credit card payment plan #
DBS loves to advertise “0% interest instalments” when you split large credit card purchases into monthly payments. Sound generous, right? Except it isn’t: the bank just swaps “interest” for an upfront “processing fee”: same animal, difference cage.

Here’s their own table (archived in Aug 2025 in case they quietly change it later):
| Tenure | One-Time Processing Fee | Effective Interest Rate |
|---|---|---|
| 3 months | 0% | 0% p.a. |
| 6 months | 3% | 10.43% p.a. |
| 12 months | 5% | 9.50% p.a. |
| 18 months | 6% | 7.86% p.a. |
| 24 months | 6% | 5.98% p.a. |
You’d have to thank one of MAS’s pro-consumer rules for the third column on this table. Notice how the “0%” marketing translates into double-digit interest rates once you factor in the fee! The EIR for the 6-month plan is the highest, despite having the lowest non-zero “one-time processing fee”. To verify DBS’s EIR number, we use the master equation for lending once again. Two types of cash flows \(c_k\) are involved here:
- the upfront “one-time processing fee” \(fL\) where \(f\) is the advertised fraction, and
- monthly instalments of \(L/N\) where \(N\) is the tenure expressed in months.
So, sum up \(F\) at \(t = 0\) along with the series of \(N\) instalments: \[ L - fL - \frac{L}{N} \sum_{k=1}^N \frac{1}{(1 + r)^{k}} = 1 - f - \frac{1 - (1 + r)^{-N}}{rN} = 0. \] Crunching the numbers with numerical methods for \(f = 0.03\) and \(N = 6\) gives us \(r \approx 10.53\%\) annualised. Wait, DBS’s number is wrong! Let’s do the same for 18 months. Let \(f = 0.06\) and \(N = 18\) and solving the equation above, we get \(r \approx 7.92\%\). DBS is wrong again! We’ll see why soon, and it’s not just a simple typo…
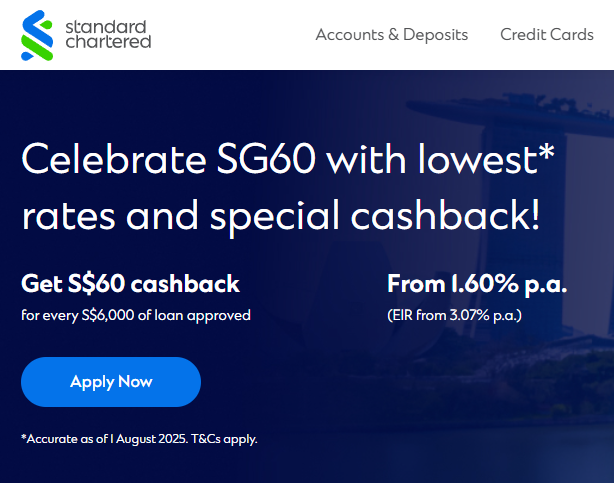
Standard Chartered’s personal loan #
Standard Chartered’s SG60 campaign for personal loan is even more confusing than the others. Let’s tear it apart.

This loan offering contains
- a cashback of \(60 \cdot \left\lfloor L / 6000 \right\rfloor\),
- an fixed upfront “processing fee” (again!) of \(199\) hidden in the finest of fine prints, and
- monthly instalments calculated from a fake “interest” rate of \(1.60\%\).
The loan package is so confusing even the disclosed EIR is wrong as it doesn’t factor in the processing fee and the cashback (though they do acknowledge this elsewhere on the page).
Let’s first see how they arrived at the wrong EIR of \(3.07\%\). Using the equation for Trust Bank and set \(N = 5 \cdot 12 = 60\), we indeed find \(r \approx 3.07\%\) annualised. As expected, ignoring the very important processing fee results in a lower than expected EIR.
Let’s do it the right way. Using the master equation of lending again, we have \[ L + 60 \left\lfloor \frac{L}{6000} \right\rfloor - 199 - L \left( \rho + \frac{1}{N} \right) \frac{1 - (1 + r)^{-N}}{r} = 0. \] Notice that the cashback has a positive sign: we can think of cashback as increasing the loan disbursement amount. Here we also assume the cashback and processing fee are transferred at time \(t = 0\). Let \(L = 20000\) and \(N = 5 \cdot 12 = 60\), we get \(r \approx 3.11\%\) per annum.
What happens if we max out the cashback? This would mean applying for a loan of \(L = 250000\), which appears to be the maximum selectable on the website. This gives rise to \(r \approx 2.71\%\) per annum, not bad!
Bonus: an unlicensed lender / loan shark #
Here’s a typical SMS you might receive on a Singaporean number:
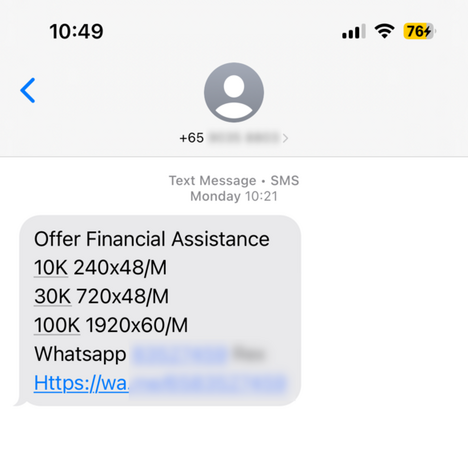
The content of the SMS is a little cryptic, but armed with finance knowledge we don’t need the Rosetta Stone to decipher it.
| Loan Amount | Monthly Payment | Tenure (months) | Total Repayment | Extra Paid |
|---|---|---|---|---|
| 10,000 | 240 | 48 | 11,520 | 1,520 |
| 30,000 | 720 | 48 | 34,560 | 4,560 |
| 100,000 | 1,920 | 60 | 115,200 | 15,200 |
The SMS doesn’t mention anything about interest rate. If we were to calculate a bank-style fake “teaser rate” for each package, it would be \[ \frac{\text{Extra Paid}}{\text{Tenure (years)}} \times \text{Loan Amount}. \] The teaser rate for the $10,000 and $30,000 loans is 3.80%, while that for the $100,000 loan is 3.04%. By now, you know that this rate is meaningless.
Writing the master equation of lending for these isn’t too hard. If \(p\) is the fixed monthly payment offered, then we simply have \[ L - p \sum_{k=1}^N \frac{1}{(1 + r)^k} = L - \frac{1 - (1 + r)^{-N}}{r} p = 0. \] With this, we find \(r \approx 7.12\%\) for the $10,000 and $30,000 loans and \(r \approx 5.71\%\) for the $100,000 loan.
Don’t calculate EIR by hand… #
In the previous section we’ve broken down the various loan offerings available in Singapore, licensed or otherwise. We’ve been invoking the master equation of lending for calculate the true cost of borrowing. But most loans are paid in fixed instalments sprinkled with an upfront fee and/or cashback. The fixed monthly payment allows us to replace the sum with a closed form. This means we can write down a more specialised variant of the master equation as \[ \boxed{L + C - F - \frac{1 - (1 + r)^{-N}}{r} p = 0}, \] where \(L\) is the loan amount, \(C\) is the cashback amount, \(F\) is the upfront fee amount, \(N\) is the tenure, \(p\) is the payment per period, and \(r\) is the EIR for one period.
We’ve talked about how there isn’t a closed form solution for this. We’ll need to resort to numerical methods, which unfortunately is extremely tedious to calculate by hand. We could instead solve for \(r\) using Newton’s method. Recall that the method proceeds by starting with a guess \(x_0\), then iteratively compute \[ x_{n+1} = x_n - \frac{f(x_n)}{f^\prime(x_n)}. \] Let \(f\) be the left hand side of the specialised equation above. Then \[ f^\prime(r) = \frac{1 - (1 + r)^{-(N + 1)} (1 + r (N + 1))}{r^2} p. \] We have everything we need to implement Newton’s method in code. The following is a zero-dependency JS code pastable into your browser developer console (Ctrl+Shift+J on Chrome):
function computeEIR(L, C, F, N, p, guess = 0.01, tol = 1e-7, maxIter = 100) {
let r = guess;
for (let i = 0; i < maxIter; ++i) {
const f = (L + C - F) / p - (1 - Math.pow(1 + r, -N)) / r;
if (Math.abs(f) < tol) {
return r;
}
const fp = (1 - Math.pow(1 + r, -(N + 1)) * (1 + r * (N + 1))) / (r * r);
if (fp === 0) {
console.error("Newton's method failed: Derivative is zero.");
return null;
}
r -= f / fp;
}
console.error("Newton's method failed to converge within the maximum number of iterations.");
return null;
}
A Python version using scipy is as follows:
from scipy.optimize import newton
def compute_eir(L, C, F, N, p, guess=0.01, tol=1e-7, max_iter=100):
f = lambda r: (L + C - F) / p - (1 - (1 + r) ** -N) / r
fprime = lambda r: (1 - (1 + r) ** (-(N + 1)) * (1 + r * (N + 1))) / (r * r)
return newton(f, x0=guess, fprime=fprime, tol=tol, maxiter=max_iter)
With the code above, we can revisit Trust Bank’s case, where we have \(F = C = 0\), and \(r\) is independent of \(L\), while \(p\) is parametrised by \(\rho\) and \(N\). The following plot how \(r\) varies as you tune the \(\rho\) and \(N\) knobs:
We see that the EIR peaks somewhere in the lower tenures, then very gradually decreases as the tenure increases. In fact, in the equation we wrote for Trust Bank, we have \[ \lim_{N \to \infty} \left( \rho + \frac{1}{N} - \frac{r}{1 - (1 + r)^{-N}} \right) = \rho - r = 0, \] implying \(\rho = r\) in the limit. This limit is correct if we assume \(r \ge 0\) which permits the \((1 + r)^{-N}\) term to vanish as \(N \to \infty\). The fact that \(\rho = r\) in the limit is largely irrelevant in practice though due to the extremely slow convergence.
DBS’s programming error #
As mentioned in our teardown of DBS’s credit card payment plan, the EIR disclosed by DBS is wrong. Have a look at their own calculator page (archived here in case they modify it silently) for personal loans:
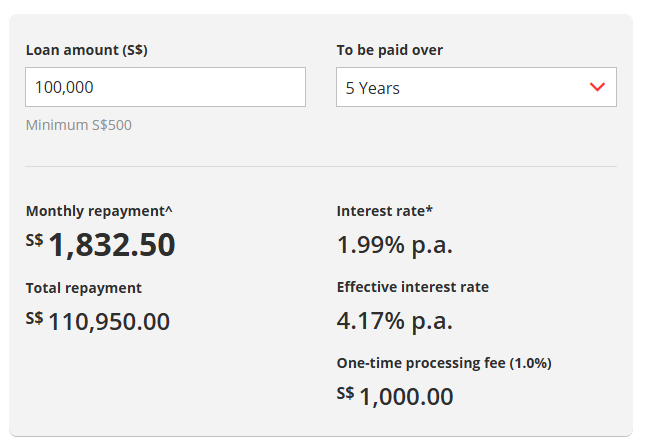
If you compute the EIR using the same inputs using the JS code I wrote above, you’ll find \(r \approx 4.21\%\) per annum. What’s going on here? Time to roll my sleeves up and reverse engineer the JS code running on DBS’s web page:
function calculateLoan() {
var loanAmount = removeCommaInNumbert($('#calc_loan_amount').val());
var loanYears = $('#calc_loan_years').val();
var processFee = 0;
var interestCharges = 0;
var monthlyChargeWithProcessFee = 0;
if (oneTimeProcessFeeFlat == 0 && oneTimeProcessFeePercentage != 0) {
processFee = (loanAmount / 100) * oneTimeProcessFeePercentage;
$('#calc_process_fee').text(
addCommaAndDecimal((loanAmount / 100) * oneTimeProcessFeePercentage)
);
} else if (oneTimeProcessFeeFlat != 0 && oneTimeProcessFeePercentage == 0) {
processFee = oneTimeProcessFeeFlat;
}
interestCharges = (loanAmount * (interestRate / 100) * (loanYears * 12)) / 12;
console.log(interestCharges);
monthlyChargeWithProcessFee =
(loanAmount + interestCharges + processFee) / (loanYears * 12);
console.log(monthlyChargeWithProcessFee);
$("#calc_month_pay").text(
addCommaAndDecimal((interestCharges + loanAmount) / (loanYears * 12))
);
var monthpay = (
((interestCharges + loanAmount).toFixed(2) / (loanYears * 12)).toFixed(2)
);
$("#calc_total_pay").text(
addCommaAndDecimal(
loanAmount + (loanAmount * (interestRate / 100) * loanYears) + processFee
)
);
$("#calc_loan_EIR").text(
(((rate((loanYears * 12), -monthlyChargeWithProcessFee, loanAmount)) * 12) * 100).toFixed(2)
);
$('#calc_summary').find('.dynamic-txt-gray').removeClass('txt-gray');
console.log('start Calculation');
}
var rate = function(nper, pmt, pv, fv, type, guess) {
// ... [omitted] ...
};
This low quality code is copied from DBS’s website but formatted for slight readability improvement. The culprit lies in here:
monthlyChargeWithProcessFee =
(loanAmount + interestCharges + processFee) / (loanYears * 12);
// ... [omitted] ...
$("#calc_loan_EIR").text(
(((rate((loanYears * 12), -monthlyChargeWithProcessFee, loanAmount)) * 12) * 100).toFixed(2)
);
Observe how the one-time (!) processing fee is split evenly into \(N\) instalments! This is rubbish! This makes the loan look cheaper than it really is. Time preference strikes again: money paid at the start has a higher time value than money paid later. Proper calculations must model the fee as an immediate cash outflow at time 0, not amortised.
What exactly is more real about EIR? #
Okay, but why should you care about EIR rather than the fake “interest” rate advertised by banks and lenders? Here’s the blunt truth: EIR is the only number that lets you compare loans to literally everything else in finance.
Imagine these two gym memberships: “10 dollars joining fee + 50 dollars/month” vs. “no joining fee + 55 dollars/month”. Which is cheaper? The joining fee is like the processing fee on a loan. EIR is the calculation that lets you compare the two fairly.
EIR captures time preference: paying 50 dollars upfront isn’t the same thing as paying 50 dollars spread over two years, because money today, which is money that can be saved, invested, spent today, is worth more than money later. EIR recognises this while the advertised fake “interest” rate doesn’t. In other words, EIR captures opportunity cost.
If your loan has an EIR of 6%, that’s your cost of capital. This means if you invest the borrowed money in an investment that yields 6% per year, your net return is exactly 0%, because all of the returns from the investment go straight to paying off the loan. EIR allows you to make an apples-to-apples comparison to other loans and investments.
This is also what banks try to hide when they plaster “0% instalments” or “1.99% flat” in big font. They’d rather you not notice the effective cost of capital is actually 7%, 9%, sometimes double digits. If you borrow at 6% EIR but invest in something that promises 4%, then it’s not worth it. EIR makes everything line up correctly.
EIR cuts through the bullshit.
We might call this a promissory note. ↩︎
Such a person is creditworthy. ↩︎
We are dividing \(r\) by 365 here as \(r\) is assumed to be an annual rate. One (but not only) way to convert it to a daily rate would just be dividing by 365. It’s common in finance to always be dividing by 365 even on a leap year. ↩︎
But subject to market forces! In practice, people are rarely able to demand a discount rate ex nihilo. ↩︎
Notice how in this equation, the sign of \(L\) is the opposite of the signs of the cash flows. This reflects the direction of cash flow: an upfront loan disbursement, followed by cash flows moving in the opposite direction. The overall left-hand side of the equation is called the net present value (NPV). ↩︎
Interestingly, Trust Bank’s online calculator does not match this exactly: it shows an EIR of 3.81%, likely due to numerical errors in whatever algorithm they’re using. ↩︎
